Hello World for Numerical Packages
Hand Coded Heat
At a Glance
| Questions | Objectives | Key Points |
|---|---|---|
| What is a numerical algorithm? | Implement a simple numerical algorithm. Use it to solve a simple science problem. | Numerical Packages are used to solve scientific problems involving PDEs. |
| What is discretization? | Introduce basic concepts in solving continuous PDEs using discrete computations. | Meshing (or discretization) is an important first step. |
| How can numerical packages help me with my software? | Understand the value numerical packages offer in developing science applications | Numerical packages offer: rigorous/vetted numerics greater generality, extreme scalability and more… |
To begin this lesson
- Open the Answers Form
- Go to the directory for the hand-coded
heatapplicationcd HandsOnLessons/hand_coded_heat
A Simple Science Question
Lets say you live in a house with exterior walls made of a single material of thickness, \(L_x\). Inside the walls are some water pipes as pictured below.
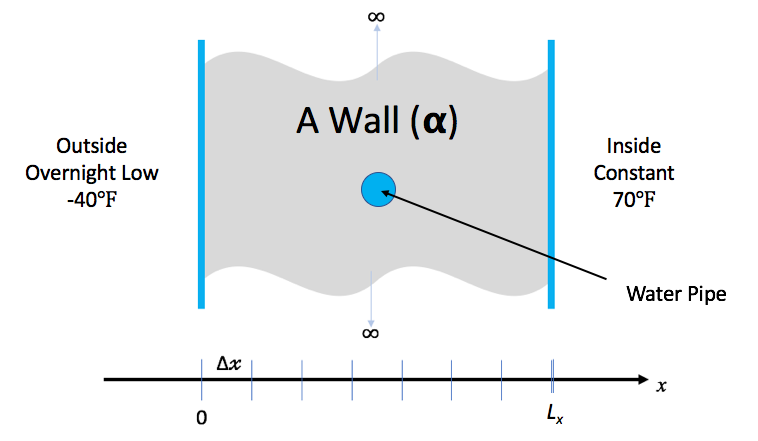
You keep the inside temperature of the house always at 70 degrees F. But, there is an overnight storm coming. The outside temperature is expected to drop to -40 degrees F for 15.5 hours. Will your pipes freeze before the storm is over?
Governing Equations
In this lesson, we demonstrate the implementation and use of a hand-coded (e.g., does not use any numerical packages) C-language application to model the one dimensional heat conduction equation through a wall as pictured here …
In general, heat conduction is governed by the partial differential (PDE)… \[\frac{\partial u}{\partial t} - \nabla \cdot \alpha \nabla u = 0\]
where u is the temperature through the wall at spatial positions, x, and times, t, \( \alpha \), is the thermal diffusivity of the material(s) comprising the wall. This equation is known as the Diffusion Equation and also the Heat Equation.
Simplifying Assumptions
To make the problem tractable for this short lesson, we make some simplifying assumptions…
- The wall can be treated as homogenous in material. In effect, we ignore the fact that part of the wall has a pipe filled with water running through it.
- The thermal diffusivity of the wall material, \( \alpha \) is constant for all space and time.
- The only heat source is from initial and/or boundary conditions.
- We will deal only with the one dimensional problem in Cartesian coordinates. That is heat along the dimension through the wall between inside and outside.
- We will discretize with constant spacing in both space, \(\Delta x\) and time, \(\Delta t\).
In this case, the PDE, above, simplifies too the one dimensional heat equation… \[\frac{\partial u}{\partial t} = \alpha \frac{\partial^2 u}{\partial x^2}\]
Discretization
The equation above is a continuous, partial differential equation (PDE) In order to write a computer program to solve this equation, numerically, the first thing we need to consider is how to discretize the equation into a form suitable for numerical computation.
Using difference equations as approximations for derivatives, we can discretize, independently, the left- and right-hand sides of equation 2. For the left-hand side, we can approximate the first derivative of u with respect to time, t, by the forward difference equation… \[\frac{\partial u}{\partial t} \Bigr\vert_{t_{k+1}} \approx \frac{u_i^{k+1}-u_i^k}{\Delta t}\]
We can approximate the right-hand side of equation 2 with the second derivative of u with respect to space, x, by the centered difference equation… \[\alpha \frac{\partial^2 u}{\partial x^2}\Bigr\vert_{x_i} \approx \alpha \frac{u_{i-1}^k-2u_i^k+u_{i+1}^k}{\Delta x^2}\]
Setting equations 3 and 4 equal to each other and re-arranging terms, we arrive at the following update scheme for producing the temperatures at the next time, k+1, from temperatures at the current time, k, as \[u_i^{k+1} = ru_{i+1}^k+(1-2r)u_i^k+ru_{i-1}^k\]
where \( r=\alpha\frac{\Delta t}{\Delta x^2} \)
In the process of discretizing the PDE, we have defined a fixed spacing in x and a fixed spacing in t as shown in the figure here
This is essentially a uniform mesh. Later lessons here address more sophisticated discretizations in space and in time which depart from these often inflexible fixed spacings.
Note that this equation now defines the value of u at time k+1 in terms of values of u at time k . This is an example of an explicit numerical method known as the Forward-Time, Centered-Space (FTCS) algorithm. As an explicit method, it has some nice properties:
- They are easy to implement.
- They typically require minimal memory.
- They are easy to parallelize.
Exercise #1: Implement the FTCS Algorithm (2-3 mins)
% ls
Double.H crankn.C ftcs.C heat.H tools utils.C
args.C exact.C heat.C makefile upwind15.C
The function, solution_update_ftcs, is defined in ftcs.C without its body.
static bool // false if unstable, true otherwise
solution_update_ftcs(
int n, // # of temperature samples in space
Double *uk1, // new temperatures @ t = k+1
Double const *uk0, // old/last temperatures @ t = k
Double alpha, // thermal diffusivity
Double dx, // spacing in space, x
Double dt, // spacing in time, t
Double bc_0, // boundary condition @ x=0
Double bc_1 // boundary condition @ x=Lx
)
{
Double const r = alpha * dt / (dx * dx);
// Sanity check for stability
if (r > 0.5) return false;
// Update the solution using FTCS algorithm
for (int i = 1; i < n-1; i++)
uk1[i] = r*uk0[i+1] + (1-2*r)*uk0[i] + r*uk0[i-1];
// Impose boundary conditions for solution indices i==0 and i==n-1
curr[0 ] = bc_0;
curr[n-1] = bc_1;
return true;
}
Edit ftcs.C and implement the FTCS numerical algorithm by coding the body of this function.
Exercise #2: Build and Test the Application (1 min)
To compile the code you have just written…
make
Getting --help from the heat Application
Run the command…
% ./heat --help
And observe the output…
Usage: ./heat <arg>=<value> <arg>=<value>...
runame="heat_results" name to give run and results dir (char*)
prec="double" precision half|float|double|quad (char*)
alpha=0.2 material thermal diffusivity (sq-meters/second) (double)
lenx=1 material length (meters) (double)
dx=0.1 x-incriment. Best if lenx/dx==int. (meters) (double)
dt=0.004 t-incriment (seconds) (double)
maxt=2 >0:max sim time (seconds) | <0:min l2 change in soln (double)
bc0=0 boundary condition @ x=0: u(0,t) (Kelvin) (double)
bc1=1 boundary condition @ x=lenx: u(lenx,t) (Kelvin) (double)
ic="const(1)" initial condition @ t=0: u(x,0) (Kelvin) (char*)
alg="ftcs" algorithm ftcs|upwind15|crankn (char*)
savi=0 save every i-th solution step (int)
save=0 save error in every saved solution (int)
outi=100 output progress every i-th solution step (int)
noout=0 disable all file outputs (int)
Examples...
./heat dx=0.01 dt=0.0002 alg=ftcs
./heat dx=0.1 bc0=273 bc1=273 ic="spikes(273,5,373)"
- The values each argument is assigned on the left are the default values the application uses when the associated argument is not specified on the command line.
- See the note below regarding more information on the
icargument to specify a variety of initial conditions.
A Simple Sanity Check Run
As a sanity check, lets just run the application with no arguments and see what happens…
% ./heat
runame="heat_results"
prec="double"
alpha=0.2
lenx=1
dx=0.1
dt=0.004
maxt=2
bc0=0
bc1=1
ic="const(1)"
alg="ftcs"
savi=0
save=0
outi=100
noout=0
Iteration 0000: last change l2=0.0909091
Iteration 0100: last change l2=2.42918e-06
Iteration 0200: last change l2=4.86446e-07
Iteration 0300: last change l2=1.00929e-07
Iteration 0400: last change l2=2.09483e-08
Iteration 0500: last change l2=4.41684e-09
Counts: Adds:24500, Mults:25001, Divs:1005, Bytes:176
Before running, the application dumps its command-line arguments so the user can see what parameters it was passed to run. In this case, you are seeing the default values. It then runs the problem as defined by the command-line arguments and saves result files to the directory specified by the runame= argument.
To list the most recently created entries in the current director, run the following command…
% ls -1t | head -n 1
heat_results
The entry heat_results is a directory containing some files created by the application. To determine what kind of files they are, run the following command…
% file heat_results/*.*
heat_results/clargs.out: ASCII text
heat_results/heat_results_soln_00000.curve: ASCII text
heat_results/heat_results_soln_final.curve: ASCII text
For this simple application, the results are uncomplicated. They are ASCII text files containing two columns of data. To see an example, run the command
% cat heat_results/heat_results_soln_final.curve
# Temperature
0 0
0.1 0.1039
0.2 0.2073
0.3 0.3101
0.4 0.4119
0.5 0.5125
0.6 0.6119
0.7 0.7101
0.8 0.8073
0.9 0.9039
1 1
The first column is each spatial position, \(x_{i}\) and the second column is the temperature, u, at that spatial position. The name of the file indicates the time of the solution data stored therein.
Testing The heat Application
Before we use our new application to solve our simple science question, how can we assure ourselves that the code we have written is not somehow seriously broken?
- Compare it to known, validated numerical solutions.
- Compare it to known analytical solutions.
- Confirm its behavior at steady state.
In any case, think about how you would measure error.
We know, maybe even intuitively, that if we maintain constant temperatures at \(A @ x=0\) and \(B @ x=L_x\), then after a long time (e.g. when the solution reaches steady state), we expect it to be a simple linear variation between temperatures A and B. For example, observe what happens after a long time in the one dimensional example below.
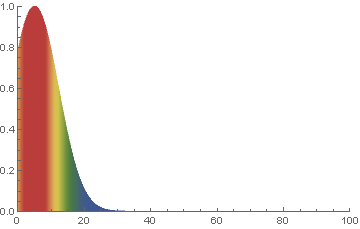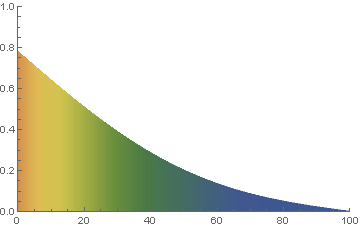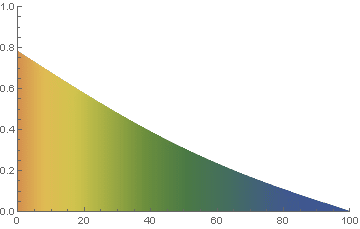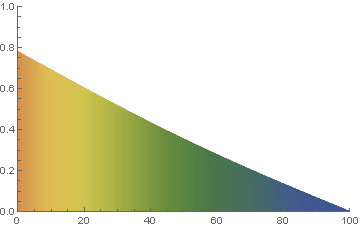
Since the default length is 1 and the default boundary conditions are 0 and 1, we just need to run the problem for a long time. But, to be a little more thorough, it is even better to start with a random initial condition too.
% ./heat dx=0.25 maxt=100 ic="rand(125489,100,50)" runame=test
Examine the initial and final results file and confirm even a random input still yields a final result where \(u=x_{i}\) for all rows of the results file
% cat test/test_soln_00000.curve
# Temperature
0 69.09
0.25 143.6
0.5 96.3
0.75 52.61
1 131.6
% cat test/test_soln_final.curve
# Temperature
0 0
0.25 0.25
0.5 0.5
0.75 0.75
1 1
Exercise #3: Use Applicaton to Model Science Problem of Interest
Lets now use our heat application to model our simple science question.
Additional Information / Assumptions
| Material | Thermal Diffusivity (sq-meters/second) |
| Wood | \(8.2 \times 10^{-8}\) |
| Adobe Brick | \(2.7 \times 10^{-7}\) |
| Common (red) Brick | \(5.2 \times 10^{-7}\) |
- Outside temp has been same as inside temp for a long time, 70 degrees F
- Night/Storm will last 15.5 hours @ -40 degrees F
- Walls are 0.25 meters thick wood and pipe is 0.1 meters in diameter
- Pipe will freeze if center point drops below freezing.
Note: An all too common issue in simulation applications is being sure data is input in the correct units. Take care!
./heat runame=wall alpha=8.2e-8 lenx=0.25 dx=0.01 dt=100 outi=100 savi=1000 maxt=55800 bc0=233.15 bc1=294.261 ic=”const(294.261)”
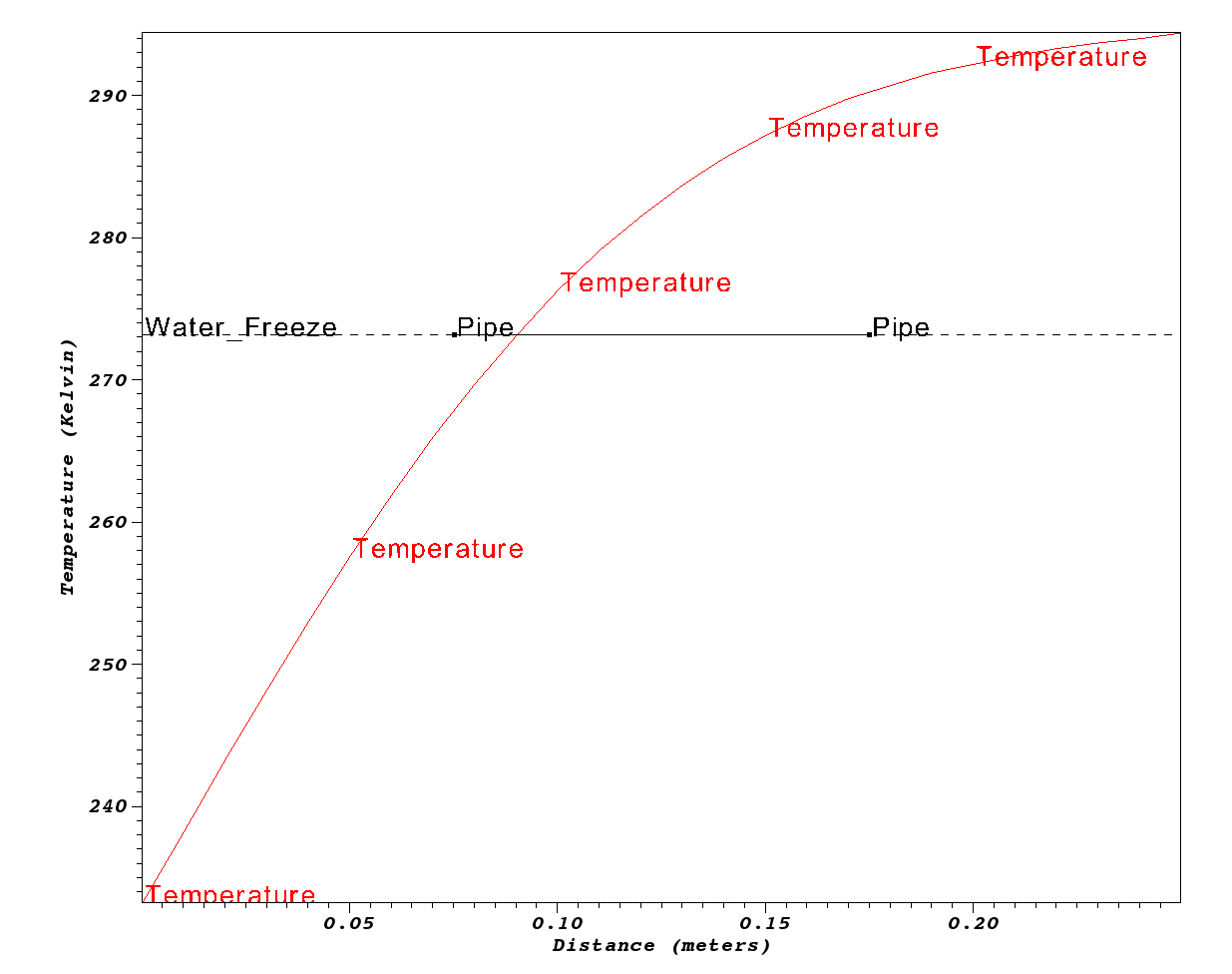
Exercise #4: Analyze Results and Do Some Science
Its time to use the results from our simulation to answer the science question of interest. Below we plot results
make plot PTOOL=gnuplot RUNAME=wall
Depending on your situation, the above command may or may not produce a plot looking like below.
No
Custom Coded Solutions are a Slippery Slope
We all like to write code and build useful tools. However, it is all too easy to see the unfamiliar as an impediment rather than enabler in reaching our sience goals. However, this is a slippery slope. We often start with relatively simple goals and over time wish to evolve our software solutions to ever more challenging science problems.
Examine the lines of code of the complete application here
$ wc -l *.[Ch]
125 args.C # User interface
94 crankn.C # Alternative solver
88 Double.H # Performance tracking
38 exact.C # Testing support
24 ftcs.C # FTCS solver
222 heat.C # Main
19 heat.H # Modularization
27 upwind15.C # Alternative solver
151 utils.C # Utilities, I/O, Data Formats
788 total
Developing generally useful science applications involves many considerations and software engineering challenges.
- More than just one spatial dimension
- More complex geometric shapes and non-cartesian coordinate systems
- Heat sources and radiation
- Laminated, anisotropic or non-linear materials
- Much larger objects involving billions of discretization points and requiring scalability in all phases of the solution.
- Parallelism such as MPI, and/or, GPU and/or many core and/or various parallel runtimes
- Alternative and interoperable discretizations, solvers, time-integrators, optimizers
- An agile and sustainable software design and implementation addressing understandability of code, with encapsulation of complexities, robustness, efficiency, scalability, portability, reproducibility, rigorous testing, etc.
When we employ numerical packages, many of these issues are addressed for us allowing us to focus more of our effort on the software engineering involved in developing applications that address our science questions of interest.
Evening Hands On Session
Short / Quick Follow-on Questions
Yes
0.3-0.4 meters
Determine Optimum Wall Thicknesses
What are the minimum thicknesses of walls of Wood, Adobe and Common brick to prevent the pipes from freezing?
When you are done, go to Intro->Submit A Show Your Work using the hands-on activity name Optimized Walls and upload evidence of your completed solution.
Compare FTCS, Crank-Nicholson and Upwind15 Algorithms (5 points)
Crank-Nicolson Discretization
Using the Crank-Nicolson discretization, we arrive at the following discretization of equation 2… \[-ru_{i+1}^{k+1}+(1+2r)u_i^{k+1}-ru_{i-1}^{k+1} = ru_{i+1}^k+(1-2r)u_i^k+ru_{i-1}^k\]
where \[r= \alpha \frac{\Delta t}{2 \Delta x^2}\]
In equation 7, the solution at spatial position i and time k+1 now depends not only on values of u at time k but also on other values of u at time k+1. This means each time we advance the solution in time we must solve a linear system; in other words we must solve for all of the values at time k+1 in one step. This is an example of an implicit method. In this case, the system of equations is tri-diagonal – since each update for u at i only uses u at i-1 , i and i+1 – so it is easier to implement than a general matrix solve but is still more complicated than an explicit update.
The code to implement this method is more involved because it involves doing a tri-diagonal solve. It is in crankn.C. It involves code that sets up and LU factors the initial matrix. Then, the LU factored matrix is used on each solution timestep to solve for the new temperatures.
Run the same problems using each of these algorithms and observe total memory usage and operation counts (printed at the end) and provide your explanations for them and in comparison with the FTCS method.
When you are done, go to Intro->Submit A Show Your Work using the hands-on activity name Crank-Nicholson and upload evidence of your completed solution.
Use The Application to Solve The Pipeline Problem (5 points)
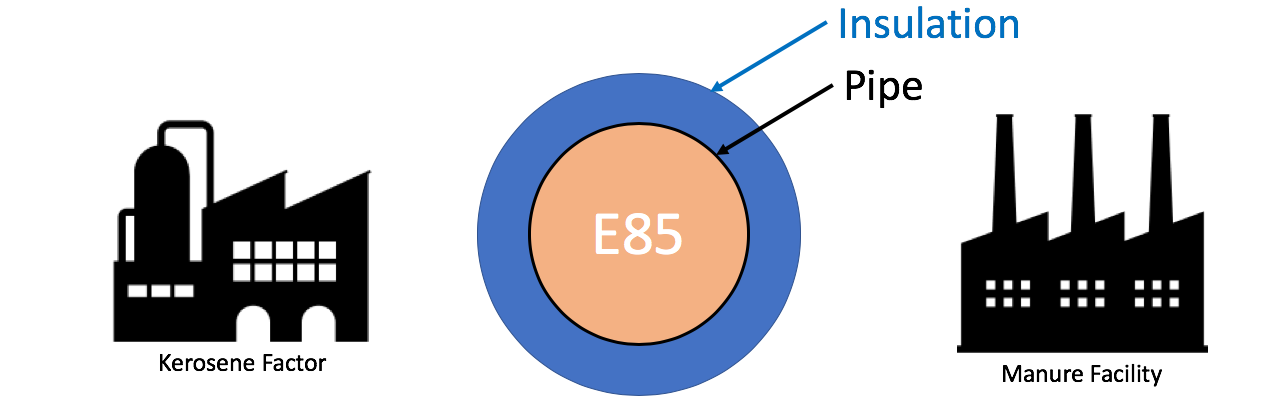
An pipeline carrying Ethenol-85 (E85) runs between a manure processing facility and a kerosene production factory. In the unlikely event that both facilities experience catastrophic explosion (burning methane at the manure facility and burning kerosene at the kerosene facility), that briefly increases the local air temperature on both sides of the pipe to the burning temperature of the respective materials, determine the minimum thermal diffusivity of the material used to coat/insulate the pipe to prevent the E-85 from exploding. Assume the pipe is 36 inches in diameter.
When you are done, go to Intro->Submit A Show Your Work using the hands-on activity name Pipeline and upload evidence of your completed solution.
Modify the Application to Support Two Materials (10 points)
Using other research, modify the application to work for a composite wall composed of two materials.
When you are done, go to Intro->Submit A Show Your Work using the hands-on activity name Composite Wall and upload evidence of your completed solution.
A note about the ic= argument to heat
The initial condition argument, ic, handles a few interesting cases
- Constant,
ic="const(V)" Set initial condition to constant value,
V- Ramp,
ic="ramp(L,R)" Set initial condition to a linear ramp having value
L@ x=0 andR@ x=\(L_x\).- Step,
ic="step(L,Mx,R)" Set initial condition to a step function having value
Lfor all x<Mx and valueRfor all x>=Mx.- Random,
ic="rand(S,B,A)" Set initial condition to random values in the range [B-A,B+A] using seed value
S.- Sin,
ic="sin(Pi*x)" Set initial condition to \(sin(\pi x)\).
- Spikes,
ic="spikes(C,A0,X0,A1,X1,...)" Set initial condition to a constant value,
Cwith any number of spikes where each spike is the pair,Aispecifying the spike amplitude andXispecifying its position in, x.

