Rank Structured Solvers

Rank-Structured Solvers with STRUMPACK

Using STRUMPACK for dense and sparse linear systems

To begin this lesson

Get into the correct directory
```
cd HandsOnLessons/strumpack
```

The problem being solved: Toeplitz matrix compression

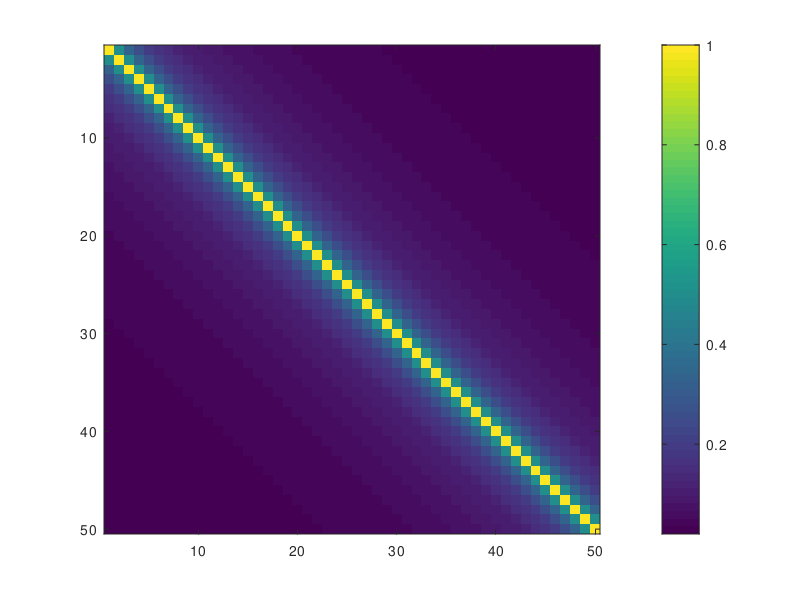
The run_testHODLR example application constructs a compressed representation of a Toeplitz matrix \[T_{i,j} = \frac{1}{1 + | i - j|}\]

using the Hierarchically Off-Diagonal Low Rank format.

T

The matrix T is constant along the diagonals and values decay rapidly going further away from the main diagonal. Off-diagonal blocks can be approximated well using low-rank. A 4-level HODLR representation looks schematically as follows:

HODLR matrix representation

where the smallest diagonal blocks are stored as dense, and all off-diagonal blocks are compressed using low-rank.

Running the Example

Run 1: Create a HODLR representation of a 20000 x 20000 matrix

$ ./run_testHODLR 20000 | tail -n 3
 Matrix construction finished
 BPACK_CheckError: fnorm: 1.7079418E+00 1.7079418E+00 acc:  1.68E-06 time:  7.37E-03
# H has max rank 12 and takes 68.2033 MByte (compared to 3200 MByte for dense storage)

Check the maximum off-diagonal block rank, the memory usage and the accuracy.

Run 2: Change the leaf size, and the compression tolerance

Change the relative compression tolerance, used for the low-rank approximation of the off-diagonal blocks

$ ./run_testHODLR 20000 --hodlr_rel_tol 1e-2 | tail -n 3
 Matrix construction finished
 BPACK_CheckError: fnorm: 2.1917744E+00 2.1917607E+00 acc:  1.09E-03 time:  7.09E-03
# H has max rank 7 and takes 60.2931 MByte (compared to 3200 MByte for dense storage)
$ ./run_testHODLR 20000 --hodlr_rel_tol 1e-8 | tail -n 3
 Matrix construction finished
 BPACK_CheckError: fnorm: 2.2692508E+00 2.2692508E+00 acc:  3.62E-10 time:  2.25E-02
# H has max rank 21 and takes 81.9533 MByte (compared to 3200 MByte for dense storage)

Note how the tolerance impacts the memory usage, the maximum rank and the accuracy of the approximation.

$ ./run_testHODLR 20000 --hodlr_leaf_size 8 | tail -n 3
 Matrix construction finished
 BPACK_CheckError: fnorm: 1.9329823E+00 1.9329820E+00 acc:  2.90E-06 time:  1.75E-02
# H has max rank 12 and takes 30.9037 MByte (compared to 3200 MByte for dense storage)
$ ./run_testHODLR 20000 --hodlr_leaf_size 128 | tail -n 3
 Matrix construction finished
 BPACK_CheckError: fnorm: 2.3231555E+00 2.3231554E+00 acc:  1.69E-06 time:  9.30E-03
# H has max rank 12 and takes 46.2892 MByte (compared to 3200 MByte for dense storage)

Check also the impact of the leaf size, the smallest blocks on the diagonal of the HODLR representation, on the memory use and the compression quality.

You can run with the –help command line option to see further tunable parameters.

3D Poisson with a fast direct solver

Next we solve the 3-dimensional Poisson equation \[\nabla^2 u = f\]

on a regular 3-dimensional grid with Dirichlet boundary conditions and a random right hand-side f, using an approximate sparse factorization solver.

Run 1: Exact sparse solver

$ mpiexec -n 1 ./run_testPoisson3d 40
# Initializing STRUMPACK
# using 12 OpenMP thread(s)
# number of tasking levels = 6 = log_2(#threads) + 3
# initial matrix:
#   - number of unknowns = 64000
#   - number of nonzeros = 438400
# nested dissection reordering:
#   - Geometric reordering
#   - strategy parameter = 8
#   - number of separators = 5545
#   - number of levels = 13
#   - nd time = 0.0120502
#   - symmetrization time = 2.45706e-06
# symbolic factorization:
#   - nr of dense Frontal matrices = 5545
#   - symb-factor time = 0.0133843
# multifrontal factorization:
#   - estimated memory usage (exact solver) = 350.843 MB
#   - factor time = 6.45393
#   - factor nonzeros = 43855344
#   - factor memory = 350.843 MB
#   - factor memory/nonzeros = 100 % of multifrontal
#   - compression = none
REFINEMENT it. 0	res =      102.762	rel.res =            1	bw.error =            1
REFINEMENT it. 1	res =  7.40334e-13	rel.res =  7.20437e-15	bw.error =  3.30291e-15
# DIRECT/GMRES solve:
#   - abs_tol = 1e-10, rel_tol = 1e-06, restart = 30, maxit = 5000
#   - number of Krylov iterations = 1
#   - solve time = 0.343346
# COMPONENTWISE SCALED RESIDUAL = 3.28441e-15

Note the factorization statistics, such as memory usage and time. The solve performs forward and backward substitution with the lower and upper sparse triangular factors respectively. Since no low-rank compression is used, the solver converges in a single iteration of iterative refinement, i.e., it acts as an exact direct solver.

Run 2: Enable Block Low Rank (BLR) compression

$ ./run_testPoisson3d 40 --sp_compression BLR
# Initializing STRUMPACK
# using 12 OpenMP thread(s)
# number of tasking levels = 6 = log_2(#threads) + 3
# initial matrix:
#   - number of unknowns = 64000
#   - number of nonzeros = 438400
# nested dissection reordering:
#   - Geometric reordering
#   - strategy parameter = 8
#   - number of separators = 5545
#   - number of levels = 13
#   - nd time = 0.0104044
#   - symmetrization time = 2.34321e-06
# symbolic factorization:
#   - nr of dense Frontal matrices = 5521
#   - nr of BLR Frontal matrices = 24
#   - symb-factor time = 0.0153996
#   - sep-reorder time = 0.0558912
# multifrontal factorization:
#   - estimated memory usage (exact solver) = 350.843 MB
#   - factor time = 3.70802
#   - factor nonzeros = 30415917
#   - factor memory = 243.327 MB
#   - factor memory/nonzeros = 69.3551 % of multifrontal
#   - compression = blr
#   - relative compression tolerance = 0.0001
#   - absolute compression tolerance = 1e-10
GMRES it. 0	res =      252.857	rel.res =            1	 restart!
GMRES it. 1	res =     0.104278	rel.res =    0.0004124
GMRES it. 2	res =  2.19998e-05	rel.res =  8.70049e-08
# DIRECT/GMRES solve:
#   - abs_tol = 1e-10, rel_tol = 1e-06, restart = 30, maxit = 5000
#   - number of Krylov iterations = 2
#   - solve time = 0.487943
# COMPONENTWISE SCALED RESIDUAL = 1.35614e-07

Now with Block Low Rank compression enabled, note again the factorization info, and see how the time and memory usage is reduced compared to the direct solver.

However, since the sparse triangular factorization is no longer exact, the approximate factorization is now used as a preconditioner for the GMRES iterative solver. With the current settings, GMRES converges in only 2 iterations, illustrating the robustness of the preconditioner. The solution phase now takes longer than it took for the direct solver setup. This illustrates the trade-off between time spent in factorization (preconditioner setup) and solve.

Now experiment with different BLR parameters

$ ./run_testPoisson3d 40 --sp_compression BLR --blr_rel_tol 1e-1
$ ./run_testPoisson3d 40 --sp_compression BLR --blr_rel_tol 1e-6
$ ./run_testPoisson3d 40 --sp_compression BLR --blr_leaf_size 16
$ ./run_testPoisson3d 40 --sp_compression BLR --blr_leaf_size 512
$ ./run_testPoisson3d 40 --sp_compression BLR --blr_rel_tol 1e-6 --help

Observe how the compression tolerance influences the GMRES convergence, the memory usage and the factorization and solve time.

Run 3: Enable HSS or HODLR compression, run in parallel

Now we switch to parallel, and enable Hierarchically Semi-Separable (HSS) or Hierarchically Off-Diagonal Low Rank approximations.

$ mpiexec -n 12 ./run_testPoisson3dMPIDist 60 --sp_compression HSS \
   --sp_compression_min_sep_size 1000 --hss_rel_tol 1e-2
$ mpiexec -n 12 ./run_testPoisson3dMPIDist 60 --sp_compression HODLR \
   --sp_compression_min_sep_size 1000 --hodlr_leaf_size 128

This will run a larger problem and enable HSS or HODLR compression. HSS compression is applied to dense sub-blocks, called frontal matrices, in the sparse triangular factors. However, this compression is only beneficial for large enough blocks, and for has too much overhead for smaller blocks. This minimum size can be tuned with the –sp_compression_min_sep_size 1000 parameter. Look in the output for the number of HSS or HODLR fronts. If this is 0, then no fronts are compressed. You can also experiment with other HSS or HODLR settings, such as relative and absolute compression tolerance and leaf size.

Out-Brief

In this lesson, we have used STRUMPACK to illustrate compression of dense rank-structured matrices. The example used was a Toeplitz matrix. Other applications include dense linear systems arising from the boundary element method for integral equations, covariance matrices, kernel matrices, etc.

We also illustrated the use of rank-structured matrix compression, such as block low rank (BLR), hierarchically off-diagonal low rank (HODLR) and hierarchically semi-separable (HSS) in sparse factorization based sparse solvers. This compression asymptotically reduces the memory requirements and number of floating point operations in sparse direct solver. However, the resulting factorization is inexact, and is typically used as a preconditioner.