Rank Structured Solvers
Rank Structured Solvers with STRUMPACK
To begin this lesson
- Enter the lesson directory
cd track-5-numerical/rank_structured_strumpack
The problem being solved: Toeplitz matrix compression
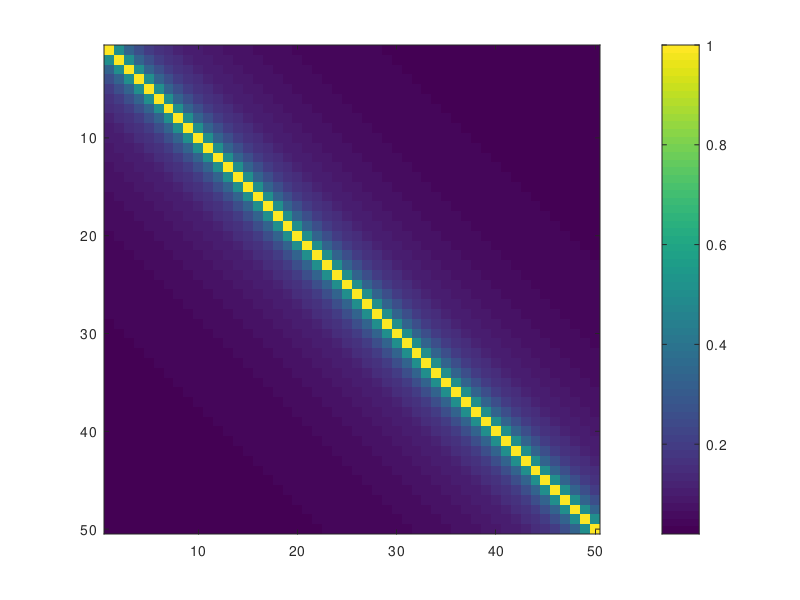
The testHODLR example application constructs a compressed representation of a Toeplitz matrix \[T_{i,j} = \frac{1}{1 + | i - j|}\]
using the Hierarchically Off-Diagonal Low Rank format.
| T |
|---|
|
The matrix T is constant along the diagonals and values decay rapidly going further away from the main diagonal. Off-diagonal blocks can be approximated well using low-rank. A 4-level HODLR representation looks schematically as follows:
| HODLR matrix representation |
|---|

|
where the smallest diagonal blocks are stored as dense, and all off-diagonal blocks are compressed using low-rank.
Running the Example
Run 1: Create an HODLR representation of a 5000 x 5000 matrix
$ ./build/testHODLR 5000
dense (2DBC) 5000 x 5000 matrix
- memory(T2d) = 200 MByte
Compression from matrix elements
HODLR
- total_nonzeros(H) = 1045127
- total_memory(H) = 8.36102 MByte
- maximum_rank(H) = 13
- ||T-H||_F/||T||_F = 2.03289e-07
- ||X-T\(T*X)||_F/||X||_F = 3.38266e-07
GMRES it. 0 res = 69.743 rel.res = 1 restart!
GMRES it. 1 res = 2.4622e-05 rel.res = 3.53039e-07
GMRES it. 2 res = 4.11533e-11 rel.res = 5.90071e-13
- ||X-A\(A*X)||_F/||X||_F = 5.90223e-13
BiCGStab it. 2 res = 104.266 rel.res = 1
BiCGStab it. 1 res = 3.53782e-11 rel.res = 3.39307e-13
- ||X-A\(A*X)||_F/||X||_F = 5.95814e-13
Check the maximum off-diagonal block rank, the memory usage and the accuracy.
Run 2: Change the leaf size, and the compression tolerance
Change the relative compression tolerance, used for the low-rank approximation of the off-diagonal blocks
$ ./build/testHODLR 5000 --structured_rel_tol 1e-2
HODLR
- total_nonzeros(H) = 735367
- total_memory(H) = 5.88294 MByte
- maximum_rank(H) = 6
- ||T-H||_F/||T||_F = 0.000965957
$ ./build/testHODLR 5000 --structured_rel_tol 1e-8
HODLR
- total_nonzeros(H) = 1321607
- total_memory(H) = 10.5729 MByte
- maximum_rank(H) = 18
- ||T-H||_F/||T||_F = 6.4152e-10
Note how the tolerance impacts the memory usage, the maximum rank and the accuracy of the approximation.
$ ./build/testHODLR 5000 --structured_leaf_size 8
HODLR
- total_nonzeros(H) = 879534
- total_memory(H) = 7.03627 MByte
- maximum_rank(H) = 13
- ||T-H||_F/||T||_F = 3.95619e-07
$ ./build/testHODLR 5000 --structured_leaf_size 128
HODLR
- total_nonzeros(H) = 1363206
- total_memory(H) = 10.9056 MByte
- maximum_rank(H) = 13
- ||T-H||_F/||T||_F = 1.54633e-07
Check also the impact of the leaf size, the smallest blocks on the diagonal of the HODLR representation, on the memory use and the compression quality.
You can run with the –help command line option to see further tunable parameters.
3D Poisson with a fast direct solver
Next we solve the 3-dimensional Poisson equation \[\nabla^2 u = f\]
on a regular 3-dimensional grid with Dirichlet boundary conditions and a random right hand-side f, using an approximate sparse factorization solver.
Run 1: Exact sparse solver
$ mpiexec -n 1 ./build/testPoisson3d 40 --sp_disable_gpu
# Initializing STRUMPACK
# using 12 OpenMP thread(s)
# number of tasking levels = 6 = log_2(#threads) + 3
# initial matrix:
# - number of unknowns = 64000
# - number of nonzeros = 438400
# nested dissection reordering:
# - Geometric reordering
# - strategy parameter = 8
# - number of separators = 5545
# - number of levels = 13
# - nd time = 0.0120502
# - symmetrization time = 2.45706e-06
# symbolic factorization:
# - nr of dense Frontal matrices = 5545
# - symb-factor time = 0.0133843
# multifrontal factorization:
# - estimated memory usage (exact solver) = 350.843 MB
# - factor time = 6.45393
# - factor nonzeros = 43855344
# - factor memory = 350.843 MB
# - factor memory/nonzeros = 100 % of multifrontal
# - compression = none
REFINEMENT it. 0 res = 102.762 rel.res = 1 bw.error = 1
REFINEMENT it. 1 res = 7.40334e-13 rel.res = 7.20437e-15 bw.error = 3.30291e-15
# DIRECT/GMRES solve:
# - abs_tol = 1e-10, rel_tol = 1e-06, restart = 30, maxit = 5000
# - number of Krylov iterations = 1
# - solve time = 0.343346
# COMPONENTWISE SCALED RESIDUAL = 3.28441e-15
Note the factorization statistics, such as memory usage and time. The solve performs forward and backward substitution with the lower and upper sparse triangular factors respectively. Since no low-rank compression is used, the solver converges in a single iteration of iterative refinement, i.e., it acts as an exact direct solver.
Run 2: Enable Block Low Rank (BLR) compression
$ ./build/testPoisson3d 40 --sp_compression BLR --sp_disable_gpu
# Initializing STRUMPACK
# using 12 OpenMP thread(s)
# number of tasking levels = 6 = log_2(#threads) + 3
# initial matrix:
# - number of unknowns = 64000
# - number of nonzeros = 438400
# nested dissection reordering:
# - Geometric reordering
# - strategy parameter = 8
# - number of separators = 5545
# - number of levels = 13
# - nd time = 0.0104044
# - symmetrization time = 2.34321e-06
# symbolic factorization:
# - nr of dense Frontal matrices = 5521
# - nr of BLR Frontal matrices = 24
# - symb-factor time = 0.0153996
# - sep-reorder time = 0.0558912
# multifrontal factorization:
# - estimated memory usage (exact solver) = 350.843 MB
# - factor time = 3.70802
# - factor nonzeros = 30415917
# - factor memory = 243.327 MB
# - factor memory/nonzeros = 69.3551 % of multifrontal
# - compression = blr
# - relative compression tolerance = 0.0001
# - absolute compression tolerance = 1e-10
GMRES it. 0 res = 252.857 rel.res = 1 restart!
GMRES it. 1 res = 0.104278 rel.res = 0.0004124
GMRES it. 2 res = 2.19998e-05 rel.res = 8.70049e-08
# DIRECT/GMRES solve:
# - abs_tol = 1e-10, rel_tol = 1e-06, restart = 30, maxit = 5000
# - number of Krylov iterations = 2
# - solve time = 0.487943
# COMPONENTWISE SCALED RESIDUAL = 1.35614e-07
Now with Block Low Rank compression enabled, note again the factorization info, and see how the time and memory usage is reduced compared to the direct solver.
However, since the sparse triangular factorization is no longer exact, the approximate factorization is now used as a preconditioner for the GMRES iterative solver. With the current settings, GMRES converges in only 2 iterations, illustrating the robustness of the preconditioner. The solution phase now takes longer than it took for the direct solver setup. This illustrates the trade-off between time spent in factorization (preconditioner setup) and solve.
Now experiment with different BLR parameters
$ ./build/testPoisson3d 40 --sp_compression BLR --blr_rel_tol 1e-1 --sp_disable_gpu
$ ./build/testPoisson3d 40 --sp_compression BLR --blr_rel_tol 1e-6 --sp_disable_gpu
$ ./build/testPoisson3d 40 --sp_compression BLR --blr_leaf_size 16 --sp_disable_gpu
$ ./build/testPoisson3d 40 --sp_compression BLR --blr_leaf_size 512 --sp_disable_gpu
$ ./build/testPoisson3d 40 --sp_compression BLR --blr_rel_tol 1e-6 --help --sp_disable_gpu
Observe how the compression tolerance influences the GMRES convergence, the memory usage and the factorization and solve time.
Run 3: Enable HSS or HODLR compression, run in parallel
Now we switch to parallel, and enable Hierarchically Semi-Separable (HSS) or Hierarchically Off-Diagonal Low Rank approximations.
$ mpiexec -n 12 ./build/testPoisson3dMPIDist 60 --sp_compression HSS \
--sp_compression_min_sep_size 1000 --hss_rel_tol 1e-2 --sp_disable_gpu
$ mpiexec -n 12 ./build/testPoisson3dMPIDist 60 --sp_compression HODLR \
--sp_compression_min_sep_size 1000 --hodlr_leaf_size 128 --sp_disable_gpu
This will run a larger problem and enable HSS or HODLR compression. HSS compression is applied to dense sub-blocks, called frontal matrices, in the sparse triangular factors. However, this compression is only beneficial for large enough blocks, and for has too much overhead for smaller blocks. This minimum size can be tuned with the –sp_compression_min_sep_size 1000 parameter. Look in the output for the number of HSS or HODLR fronts. If this is 0, then no fronts are compressed. You can also experiment with other HSS or HODLR settings, such as relative and absolute compression tolerance and leaf size.
Out-Brief
In this lesson, we have used STRUMPACK to illustrate compression of dense rank-structured matrices. The example used was a Toeplitz matrix. Other applications include dense linear systems arising from the boundary element method for integral equations, covariance matrices, kernel matrices, etc.
We also illustrated the use of rank-structured matrix compression, such as block low rank (BLR), hierarchically off-diagonal low rank (HODLR) and hierarchically semi-separable (HSS) in sparse factorization based sparse solvers. This compression asymptotically reduces the memory requirements and number of floating point operations in sparse direct solver. However, the resulting factorization is inexact, and is typically used as a preconditioner.
Further Reading
A good overview if rank-structured matrix formats and their use in sparse solvers can be found in Theo Mary’s Ph.D thesis.
