Role and Use of Direct Solvers in Ill-Conditioned Problems

Sparse, Direct Solvers

At A Glance

Questions	Objectives	Key Points
1. Why use a direct solver?	Understand accuracy	Direct solvers are robust for difficult problems
2. What effects direct solve performance ?	Understand ordering options	Time & space performance can vary a lot.

To begin this lesson

Open the Answers Form
Get into the correct directory
```
cd HandsOnLessons/superlu_mfem
```
The problem being solved

The convdiff.c application is modeling the steady state convection-diffusion equation in 2D with a constant velocity. This equation is used to model the concentration of something like a die in a moving fluid as it diffuses and flows through he fluid. The equation is as follows: \[\nabla \cdot (\kappa \nabla u) - \nabla \cdot (\overrightarrow{v}u)+R=0\]

Where u is the concentration that we are tracking, \(\kappa\), is the diffusion rate, v is the velocity of the flow and R is a concentration source.

In the application we use here, the velocity vector direction is fixed in the +x direction. However, the magnitude is set by the user (default of 100), \(\kappa\), is fixed at 1.0, and the source is 0.0 everywhere except for a small square centered at the middle of the domain where it is 1.0.

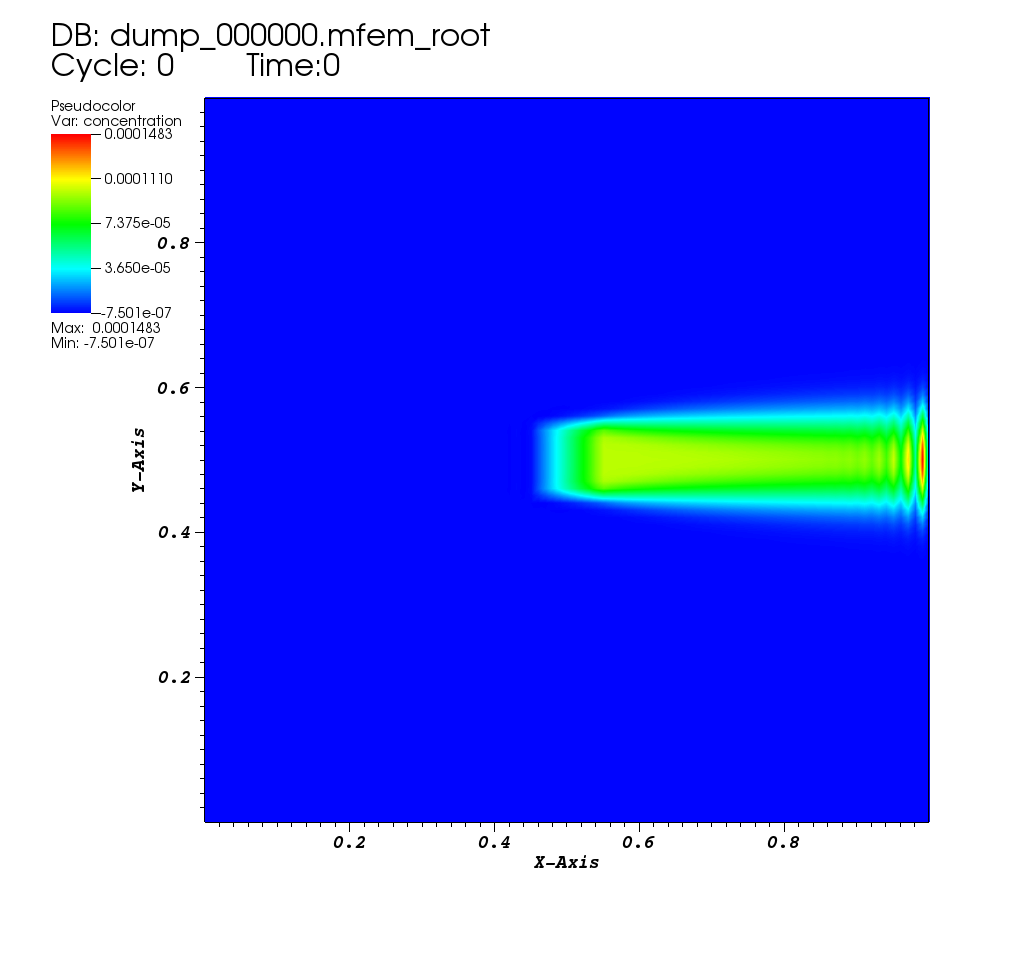
Initial Condition

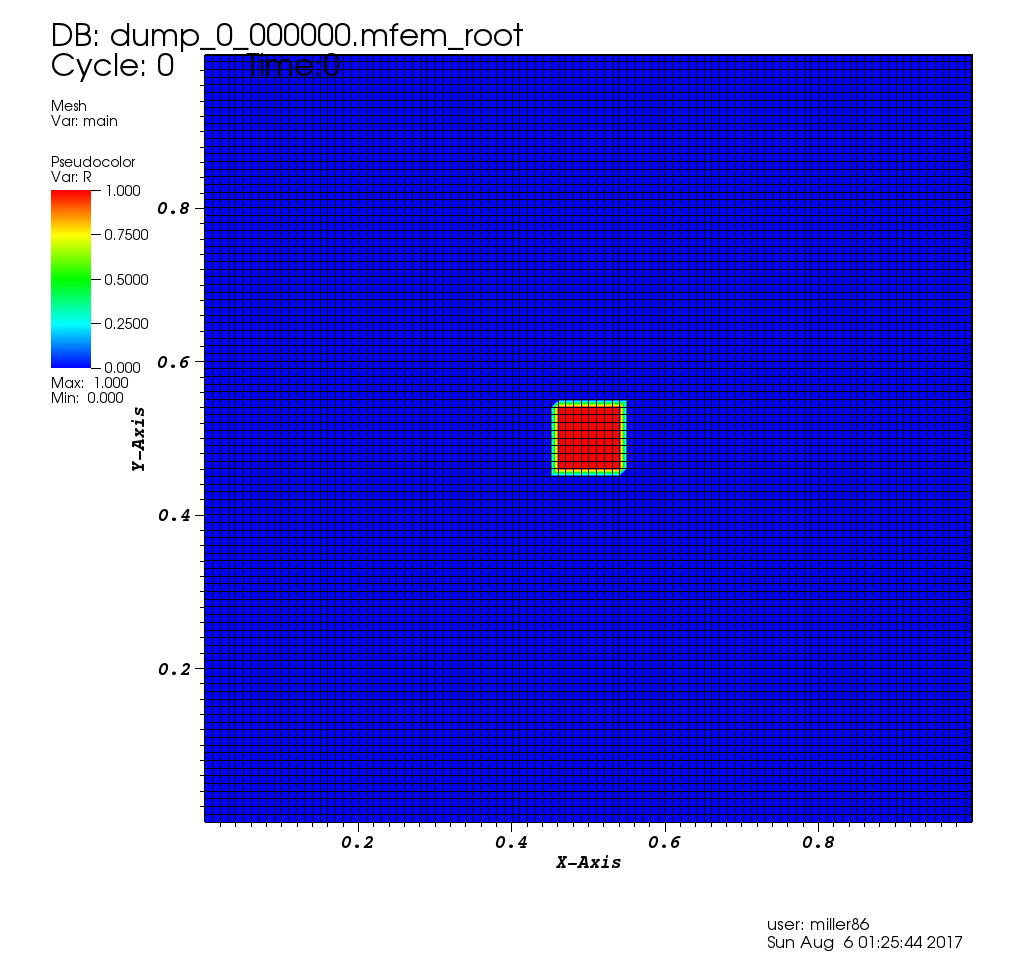Solving this PDE is well known to cause convergence problems for iterative solvers, for larger v. We use MFEM as a vehicle to demonstrate the use of a distributed, direct solver, SuperLU_DIST, to solve very ill-conditioned linear systems.

Running the Example

Run 1: default setting with GMRES solver, preconditioned by hypre, velocity = 100

$ ./convdiff | tail -n 3
Time required for first solve:  0.0408995 (s)
Final L2 norm of residual: 2.43686e-16

Steady State

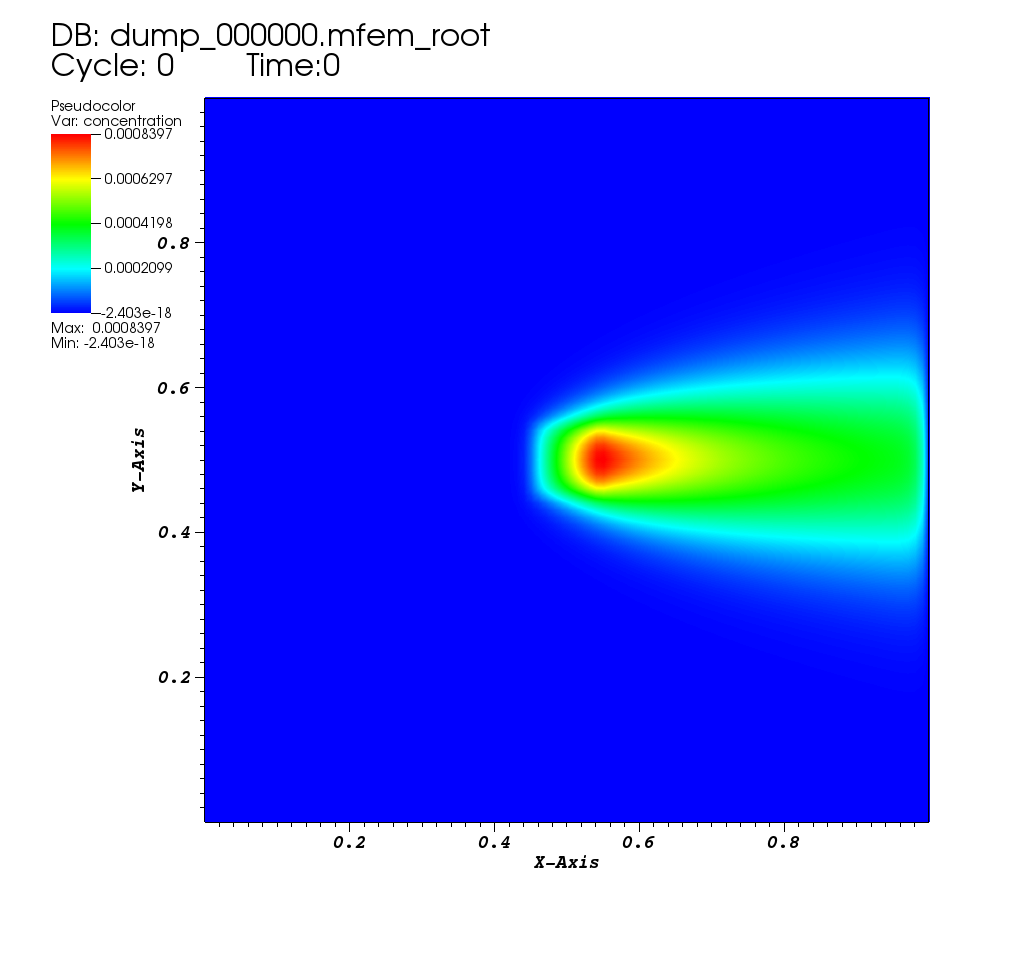Run 2: increase velocity to 1000, GMRES does not converge anymore

$ ./convdiff --velocity 1000 | tail -n 3
Time required for first solve:  0.47337 (s)
Final L2 norm of residual: 0.00095

How many orders of magnitude different is L2 norm of the residual as compared to the previous run?

Between 12 and 13

Below, we plot behavior of the GMRES method for velocity values in the range [100,1000] at increments, dv, of 25 and also show an animation of the solution GMRES gives as velocity increases

Solutions @dv=25 in [100,1000]	Contours of Solution @ vel=1000

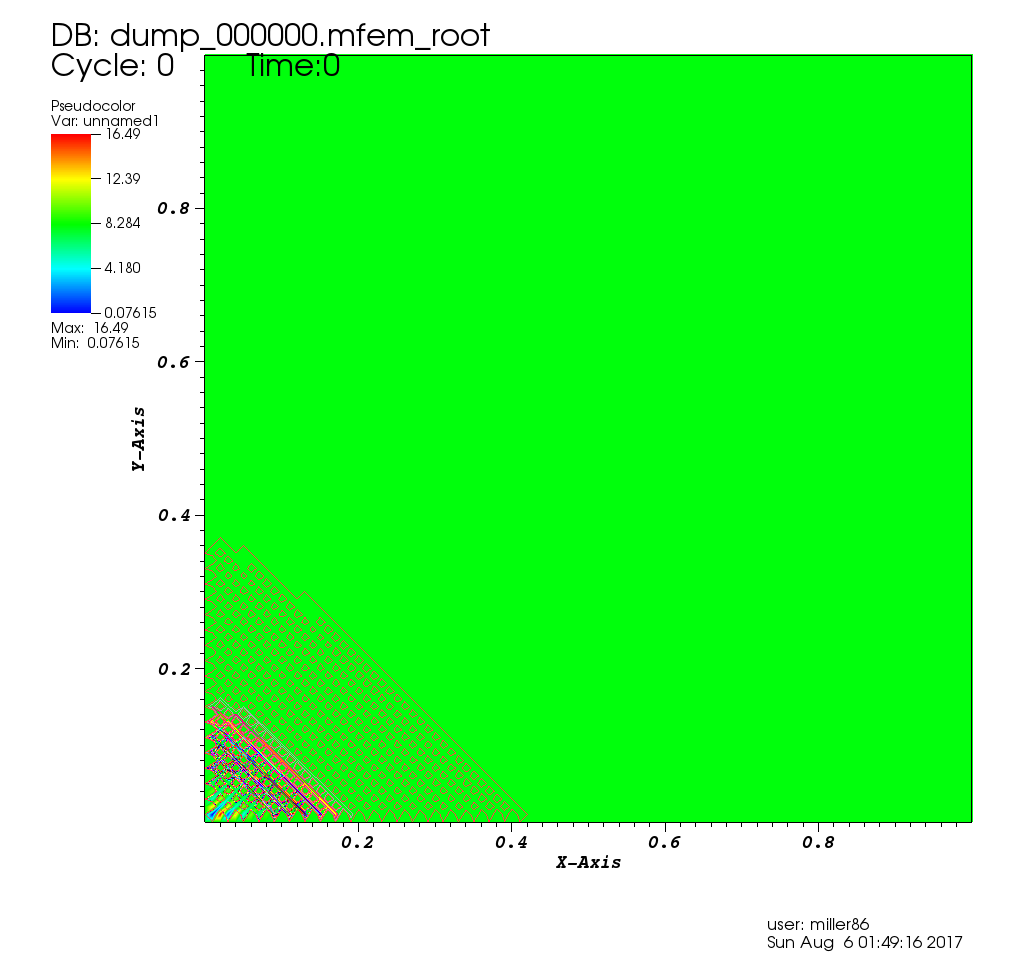Time to Solution	L2 norm of final residual

What do you think happened?

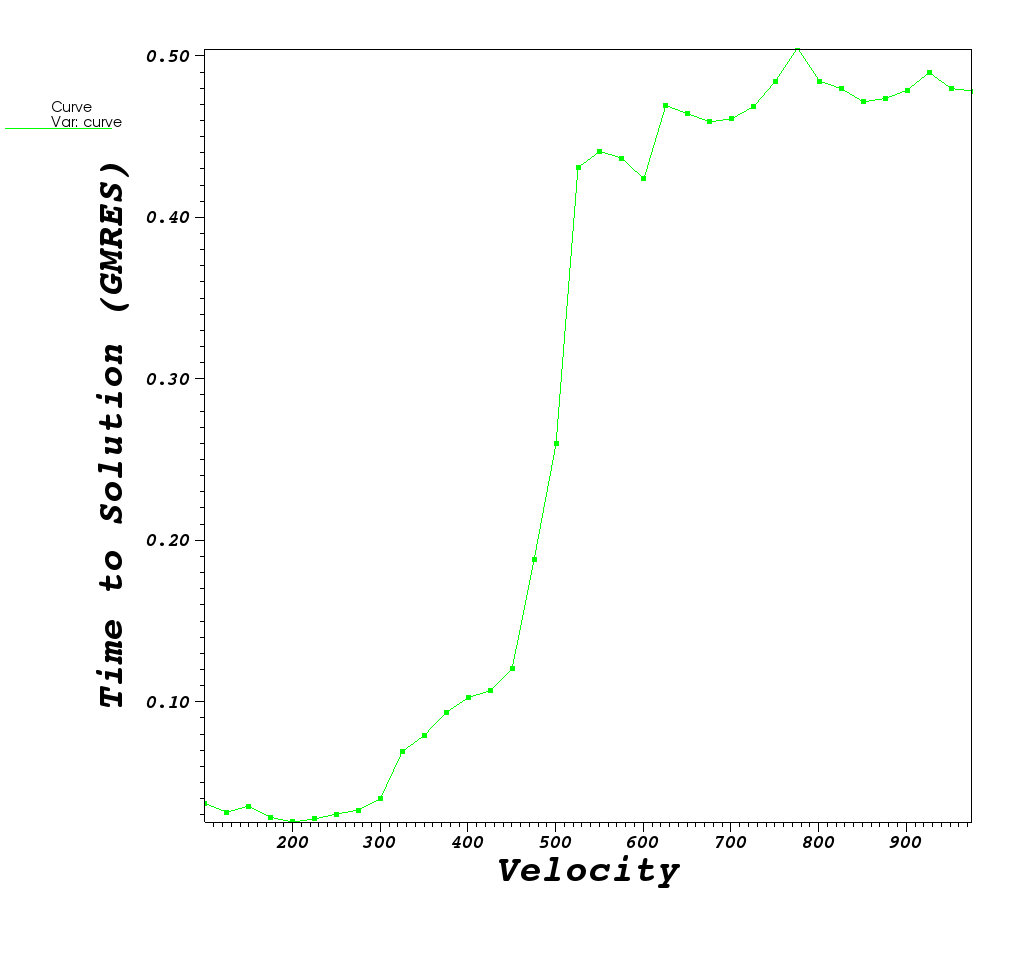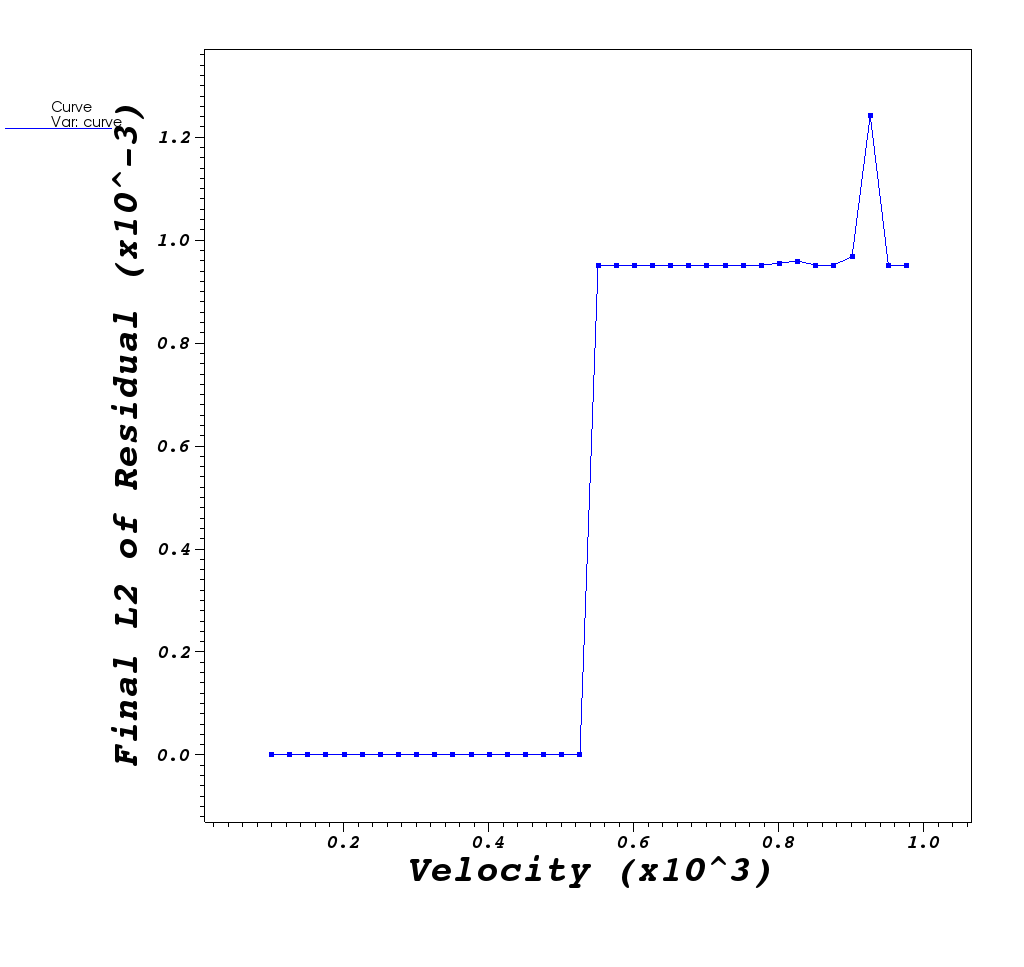GMRES method works ok for low velocity values. As velocity increases, GMRES method eventually crosses a threshold where it can no longer provide a useful result

Why does time to solution show smoother transition than L2 norm?

As instability is approached, more GMRES iterations are required to reach desired norm. So GMRES is still able to manage the solve and achieve a near-zero L2 norm. It just takes more and more iterations. Once GMRES is unable to solve the L2 norm explodes.

Run 3: Now use SuperLU_DIST, with “natural ordering”

$  ./convdiff --velocity 1000 -slu -cp 0  
Options used:
   --refine 0
   --order 1
   --velocity 1000
   --no-visit
   --superlu
   --slu-colperm 0
   --slu-rowperm 1
   --slu-parsymbfact 0
   --one-matrix
   --one-rhs
Number of unknowns: 10201
	Nonzeros in L       1040781
	Nonzeros in U       1045632
	nonzeros in L+U     2076212
	nonzeros in LSUB    1040215

** Memory Usage **********************************
** NUMfact space (MB): (sum-of-all-processes)
    L\U :           41.12 |  Total :    50.74
** Total highmark (MB):
    Sum-of-all :    50.74 | Avg :    50.74  | Max :    50.74
**************************************************
Time required for first solve:  19.0018 (s)
Final L2 norm of residual: 1.62703e-18

**************************************************
**** Time (seconds) ****
	EQUIL time             0.00
	ROWPERM time           0.01
	SYMBFACT time          0.04
	DISTRIBUTE time        0.11
	FACTOR time           18.52
	Factor flops	1.958603e+08	Mflops 	   10.58
	SOLVE time             0.10
	Solve flops	5.167045e+06	Mflops 	   52.21
	REFINEMENT time        0.20	Steps       2

**************************************************

Stead State For vel=1000

Run 4: Now use SuperLU_DIST, with MMD(A’+A) ordering.

$ ./convdiff --velocity 1000 -slu -cp 2
Options used:
   --refine 0
   --order 1
   --velocity 1000
   --no-visit
   --superlu
   --slu-colperm 2
   --slu-rowperm 1
   --slu-parsymbfact 0
   --one-matrix
   --one-rhs
Number of unknowns: 10201
	Nonzeros in L       594238
	Nonzeros in U       580425
	nonzeros in L+U     1164462
	nonzeros in LSUB    203857

** Memory Usage **********************************
** NUMfact space (MB): (sum-of-all-processes)
    L\U :           10.07 |  Total :    15.52
** Total highmark (MB):
    Sum-of-all :    15.52 | Avg :    15.52  | Max :    15.52
**************************************************
Time required for first solve:  0.111105 (s)
Final L2 norm of residual: 1.53726e-18

**************************************************
**** Time (seconds) ****
	EQUIL time             0.00
	ROWPERM time           0.01
	COLPERM time           0.04
	SYMBFACT time          0.01
	DISTRIBUTE time        0.02
	FACTOR time            0.05
	Factor flops	1.063303e+08	Mflops 	 2045.75
	SOLVE time             0.00
	Solve flops	2.367059e+06	Mflops 	  779.35
	REFINEMENT time        0.01	Steps       2

**************************************************

NOTE: the number of nonzeros in L+U is much smaller than natural ordering. This affects the memory usage and runtime.

Run 5: Now use SuperLU_DIST, with Metis(A’+A) ordering.

$ ./convdiff --velocity 1000 -slu -cp 4
Options used:
   --refine 0
   --order 1
   --velocity 1000
   --no-visit
   --superlu
   --slu-colperm 4
   --slu-rowperm 1
   --slu-parsymbfact 0
   --one-matrix
   --one-rhs
Number of unknowns: 10201
	Nonzeros in L       522306
	Nonzeros in U       527748
	nonzeros in L+U     1039853
	nonzeros in LSUB    218211

** Memory Usage **********************************
** NUMfact space (MB): (sum-of-all-processes)
    L\U :            9.24 |  Total :    14.96
** Total highmark (MB):
    Sum-of-all :    14.96 | Avg :    14.96  | Max :    14.96
**************************************************
Time required for first solve:  0.152424 (s)
Final L2 norm of residual: 1.51089e-18

**************************************************
**** Time (seconds) ****
	EQUIL time             0.00
	ROWPERM time           0.01
	COLPERM time           0.05
	SYMBFACT time          0.01
	DISTRIBUTE time        0.02
	FACTOR time            0.05
	Factor flops	7.827314e+07	Mflops 	 1717.18
	SOLVE time             0.00
	Solve flops	2.120276e+06	Mflops 	  606.75
	REFINEMENT time        0.01	Steps       2

**************************************************

Solutions @dv=25 in [100,1000]	Steady State Solution @ vel=1000

Run 5.5: Now use SuperLU_DIST, with Metis(A’+A) ordering, using 1 MPI tasks, on a larger problem.

By adding --refine 3, each element in the mesh is subdivided twice yielding a 64x larger problem. But, we’ll run it on only one processor.

$ mpiexec -n 1 ./convdiff --refine 3 --velocity 1000 -slu -cp 4
Options used:
   --refine 3
   --order 1
   --velocity 1000
   --no-visit
   --superlu
   --slu-colperm 4
   --slu-rowperm 1
   --slu-parsymbfact 0
   --one-matrix
   --one-rhs
Number of unknowns: 641601
	Nonzeros in L       40412796
	Nonzeros in U       40412796
	nonzeros in L+U     80183991
	nonzeros in LSUB    15748820

** Memory Usage **********************************
** NUMfact space (MB): (sum-of-all-processes)
    L\U :          701.82 |  Total :   758.92
** Total highmark (MB):
    Sum-of-all :   786.78 | Avg :   786.78  | Max :   786.78
**************************************************
Time required for first solve:  18.8951 (s)
Final L2 norm of residual: 5.99013e-18

**************************************************
**** Time (seconds) ****
	EQUIL time             0.03
	ROWPERM time           0.29
	COLPERM time           4.83
	SYMBFACT time          0.32
	DISTRIBUTE time        1.58
	FACTOR time            9.87
	Factor flops	2.326266e+10	Mflops 	 2357.24
	SOLVE time             0.41
	Solve flops	1.604473e+08	Mflops 	  395.95
	REFINEMENT time        0.90	Steps       2
**************************************************

Run 6: Now use SuperLU_DIST, with Metis(A’+A) ordering, using 16 MPI tasks, on a larger problem.

Here, we’ll re-run the above except on 16 tasks and just grep the output form some key values of interest.

$ ${MPIEXEC_OMPI} -n 16 ./convdiff --refine 3 --velocity 1000 -slu --slu-colperm 4 >& run6.out
Options used:
   --refine 3
   --order 1
   --velocity 1000
   --no-visit
   --superlu
   --slu-colperm 4
   --slu-rowperm 1
   --slu-parsymbfact 0
   --one-matrix
   --one-rhs
Number of unknowns: 641601
	Nonzeros in L       40340620
	Nonzeros in U       40340620
	nonzeros in L+U     80039639
	nonzeros in LSUB    15901421

** Memory Usage **********************************
** NUMfact space (MB): (sum-of-all-processes)
    L\U :          705.31 |  Total :   974.93
** Total highmark (MB):
    Sum-of-all :  2888.58 | Avg :   180.54  | Max :   180.54
**************************************************
Time required for first solve:  9.10544 (s)
Final L2 norm of residual: 2.29801e-39

**************************************************
**** Time (seconds) ****
	EQUIL time             0.03
	ROWPERM time           0.36
	COLPERM time           5.57
	SYMBFACT time          0.37
	DISTRIBUTE time        0.30
	FACTOR time            1.62
	Factor flops	2.301228e+10	Mflops 	14226.55
	SOLVE time             0.14
	Solve flops	1.623936e+08	Mflops 	 1148.60
	REFINEMENT time        0.30	Steps       2

Can you explain the processor times relative to the previous, single processor run?

We have increased the mesh size by 8x here. The matrix dimension goes up as the SQUARE of the mesh size and this accounts for 64x factor of DOFs. We have also added 16x processors. The parallel runtime is 9.10544 seconds.

Run 7: Now use SuperLU_DIST, solve the systems with same A, but different right-hand side b.

Here, we solve a different linear system but with the same coefficient matrix A. We tell SuperLU to re-use the exisiting LU factors, but only give a different right-hand side. Notice the improvement in solve time when re-using the factors.

$ mpiexec -n 16 ./convdiff --refine 3 --velocity 1000 -slu -cp 4 -2rhs
Options used:
   --refine 3
   --order 1
   --velocity 1000
   --no-visit
   --superlu
   --slu-colperm 4
   --slu-rowperm 1
   --slu-parsymbfact 0
   --one-matrix
   --two-rhs
Number of unknowns: 641601
	Nonzeros in L       40340620
	Nonzeros in U       40340620
	nonzeros in L+U     80039639
	nonzeros in LSUB    15901421

** Memory Usage **********************************
** NUMfact space (MB): (sum-of-all-processes)
    L\U :          705.31 |  Total :   974.93
** Total highmark (MB):
    Sum-of-all :  2888.58 | Avg :   180.54  | Max :   180.54
**************************************************
Time required for first solve:  9.11672 (s)
Final L2 norm of residual: 2.14235e-39

**************************************************
**** Time (seconds) ****
	EQUIL time             0.04
	ROWPERM time           0.36
	COLPERM time           5.64
	SYMBFACT time          0.38
	DISTRIBUTE time        0.23
	FACTOR time            1.61
	Factor flops	2.301228e+10	Mflops 	14307.11
	SOLVE time             0.14
	Solve flops	1.623936e+08	Mflops 	 1147.81
	REFINEMENT time        0.30	Steps       2

**************************************************
Time required for second solve (new rhs):  0.46439 (s)
Final L2 norm of residual: 1.95236e-39

	SOLVE time             0.14
	Solve flops	1.623936e+08	Mflops 	 1202.77
	REFINEMENT time        0.29	Steps       2

**************************************************

Out-Brief

In this lesson, we have used MFEM as a vehicle to demonstrate the value of direct solvers from the SuperLU_DIST numerical package.